Practitioner's Tool / Slope and Topography
The slope and topography of the site will have an impact upon the location of wastewater treatment and disposal systems. It will determine if and where pumping systems are required, and if so, the distance and elevation rise required, which will relate directly to pump size.
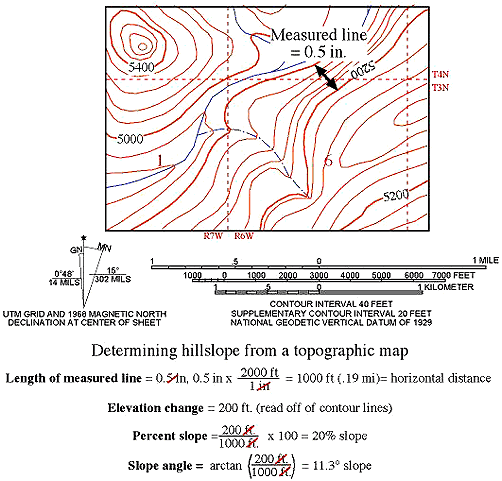
Calculating a Slope
Determining the average slope of a hill using a topographic map is fairly simple. Slope can be given in two different ways--a percent gradient or an angle of the slope. The initial steps to calculating slope either way are the same.
- Decide on an area for which you want to calculate the slope (note, it should be an area where the slope direction does not change; do not cross the top of a hill or the bottom of a valley).
- Once you have decided on an area of interest, on a map of the area, draw a straight line perpendicular to the contours on the slope. For the greatest accuracy, start and end your line on, rather than between, contours on the map.
- Measure the length of the line you drew and, using the scale of the map, convert that distance to feet.
- Determine the total elevation change along the line you drew (subtract the elevation of the lowest contour used from the elevation of the highest contour used). You do not need to do any conversions on this measurement, as it is a real-world elevation change.
To calculate a percent slope, simply divide the elevation change in feet by the distance of the line you drew (after converting it to feet). Multiply the resulting number by 100 to get a percentage value equal to the percent slope of the hill. If the value you calculate is, for example, 20, then what this means is that for every 100 feet you cover in a horizontal direction, you will gain (or lose) 20 feet in elevation.
To calculate the angle of the slope, divide the elevation change in feet by the distance of the line you drew (after converting it to feet). This is the tangent value for the angle of the slope. Apply an arctangent function to this value to obtain the angle of the slope (hit the ‘inv’ button and then the ‘tan’ button on most scientific calculators to get the slope angle). The angle you calculated is the angle between a horizontal plane and the surface of the hill.
For more information, visit the Idaho State Universitie's guide.